STK_Funct_betaRatio.cpp File Reference

In this file we implement functions around the Beta ratio function. More...

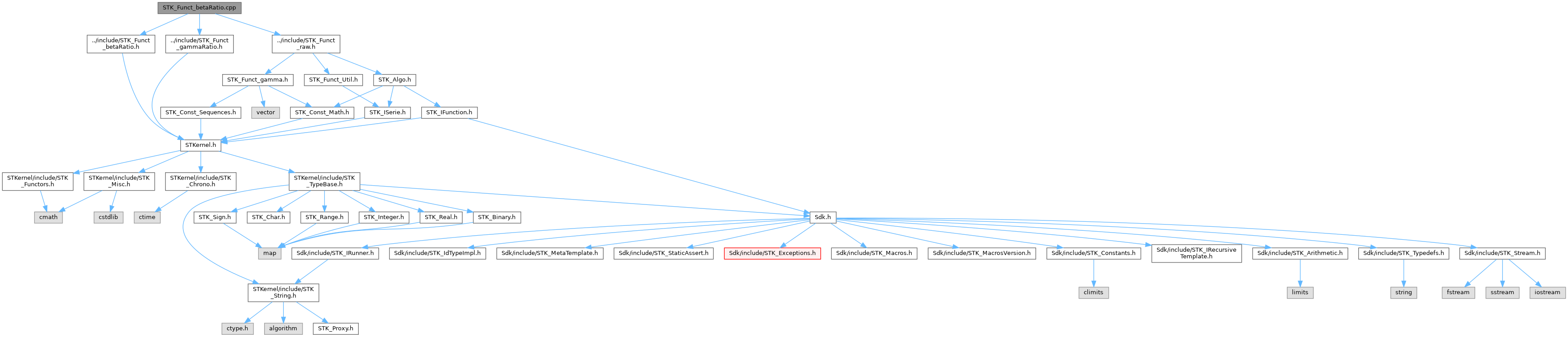
#include "../include/STK_Funct_betaRatio.h"
#include "../include/STK_Funct_gammaRatio.h"
#include "../include/STK_Funct_raw.h"

Include dependency graph for STK_Funct_betaRatio.cpp:

Go to the source code of this file.

Namespaces
namespace	STK
	The namespace STK is the main domain space of the Statistical ToolKit project.
namespace	STK::Funct
	The namespace Funct enclose all usual and special functions.

Macros
#define	d1(z)   (0.5)
#define	d2(z)   (z/8. - 0.05)
#define	d3(z)   (z*(z/48.-1./40.)+1./105.)
#define	d4(z)   (z*(z*(z/384.-1./160.)+101./16800.)-3./1400.)
#define	d5(z)
#define	d6(z)
#define	d7(z)
#define	d8(z)

Functions
Real	STK::Funct::betaRatio_ae (Real const &a, Real const &b, Real const &x, bool xm1, bool lower_tail)
	Compute the incomplete beta function ratio I_x(a,b) using the asymptotic expansion method.
Real	STK::Funct::betaRatio_sr (Real const &a, Real const &b, Real x, bool xm1, bool lower_tail)
	Compute the incomplete beta function ratio I_x(a,b) using its series representation.
Real	STK::Funct::betaRatio_up (Real const &a, Real const &b, Real const &x, bool xm1, bool lower_tail)
	Compute the incomplete beta function ratio I_x(a,b) using its recurrence formula and its asymptotic expansion.
Real	STK::Funct::betaRatio_cf (Real const &a, Real const &b, Real x, bool xm1, bool lower_tail=true)
	Compute the incomplete beta function ratio using the continued fraction method.
Real	STK::Funct::betaRatio_se (Real const &a, Real const &b, Real const &x, bool xm1, bool lower_tail)
	Compute the incomplete beta function ratio I_x(a,b) using the serie expansion method.
Real	STK::Funct::betaRatio (Real const &a, Real const &b, Real const &x, bool lower_tail=true)
	Compute the incomplete beta function ratio Compute the beta ratio function.
Real	STK::Funct::betaRatio_raw (Real const &a, Real const &b, Real const &x, bool lower_tail)

Detailed Description

In this file we implement functions around the Beta ratio function.

Definition in file STK_Funct_betaRatio.cpp.

Macro Definition Documentation

d1

#define d1

(

z

)

(0.5)

Definition at line 42 of file STK_Funct_betaRatio.cpp.

d2

#define d2

(

z

)

(z/8. - 0.05)

Definition at line 43 of file STK_Funct_betaRatio.cpp.

d3

#define d3

(

z

)

(z*(z/48.-1./40.)+1./105.)

Definition at line 44 of file STK_Funct_betaRatio.cpp.

d4

#define d4

(

z

)

(z*(z*(z/384.-1./160.)+101./16800.)-3./1400.)

Definition at line 45 of file STK_Funct_betaRatio.cpp.

d5

#define d5

(

z

)

Value:

              (z*(z*(z*(z/3840.-1./960.)+61./33600.)-13./8400.) \
              +1./1925.)

Definition at line 46 of file STK_Funct_betaRatio.cpp.

{
 
namespace Funct
{
 
Real betaRatio_ae( Real const& a, Real const& b, Real const& x
                 , bool xm1, bool lower_tail
                 )
{
#ifdef STK_BETARATIO_DEBUG
  stk_cout << _T("BetaRatio_ae(") << a << _T(", ") << b << _T(", ") << x << _T(")\n");
#endif
  // Compute b-1
  Real bm1 = b-1;
  // compute \nu = a+(b-1)/2
  Real nu = a+bm1/2.;
  // compute D = -\nu*log(x)
  Real D = (xm1 ? -log1p(-x) : -log(x)) * nu;
  // check trivial case
  if (D == 0.) return lower_tail ? 1. : 0.;
  if (Arithmetic<Real>::isInfinite(D)) return lower_tail ? 0. : 1.;
  // compute 12*\nu^2
  nu *= 12*nu;
  // variables for the series
  Real term = 1.;
  Real ak_term = 1.;
  Real a_k = 1.;
  // numerator and denominator
  Real den = term;
  Real num = 0.;
  // update term
  term *= bm1;
  // Generalized bernouilli coefs
  // coef 1 (d_1 = 1/2)
  term *= (b)*(b+1)/nu;
  Real coef = term/2; // d_1 = 1/2
  den += coef;
  a_k += (ak_term *= D/(b+1));
  num += coef * a_k;
  // coef 2
  term *= (b+2)*(b+3)/nu;
  coef = d2(bm1)*term;
  den += coef;
  a_k += (ak_term *= D/(b+2));
  a_k += (ak_term *= D/(b+3));
  num += coef * a_k;
  // coef 3
  term *= (b+4)*(b+5)/nu;
  coef = d3(bm1)*term;
  den += coef;
  a_k += (ak_term *= D/(b+4));
  a_k += (ak_term *= D/(b+5));
  num += coef * a_k;
  // coef 4
  term *= (b+6)*(b+7)/nu;
  coef = d4(bm1)*term;
  den += coef;
  a_k += (ak_term *= D/(b+6));
  a_k += (ak_term *= D/(b+7));
  num += coef * a_k;
  // coef 5
  term *= (b+8)*(b+9)/nu;
  coef = d5(bm1)*term;
  den += coef;
  a_k += (ak_term *= D/(b+8));
  a_k += (ak_term *= D/(b+9));
  num += coef * a_k;
  // coef 6
  term *= (b+10)*(b+11)/nu;
  coef = d6(bm1)*term;
  den += coef;
  a_k += (ak_term *= D/(b+10));
  a_k += (ak_term *= D/(b+11));
  num += coef * a_k;
  // coef 7
  term *= (b+12)*(b+13)/nu;
  coef = d7(bm1)*term;
  den += coef;
  a_k += (ak_term *= D/(b+12));
  a_k += (ak_term *= D/(b+13));
  num += coef * a_k;
  // coef 8
  term *= (b+14)*(b+15)/nu;
  coef = d8(bm1)*term;
  den += coef;
  a_k += (ak_term *= D/(b+14));
  a_k += (ak_term *= D/(b+15));
  num += coef * a_k;
  // result (P or Q ?)
  return lower_tail ? gammaRatioQ(b, D)
                    + (num / den) * poisson_pdf_raw(b, D)
                    : gammaRatioP(b, D)
                    - (num / den) * poisson_pdf_raw(b, D);
}
 
Real betaRatio_sr( Real const& a, Real const& b, Real x
                        , bool xm1, bool lower_tail
                        )
{
#ifdef STK_BETARATIO_DEBUG
  stk_cout << _T("BetaRatio_sr(") << a << _T(", ") << b << _T(", ") << x << _T(")\n");
#endif
  // constants
  Real s = a+b, sx = s*x, sy = s*(1-x);
  // compute B(a,b,x,y) = \frac{\Gamma(a+b)}{\Gamma(a) \Gamma(b)} x^{a}
  Real bt = ( Const::_1_SQRT2PI_*sqrt((a*b)/s)
            * exp( ( lgammaStirlingError(s)
                    -(lgammaStirlingError(a)+lgammaStirlingError(b))
                   )
                 + (xm1 ? sy- (dev0(a, sy) + dev0(b, s)) : sx- (dev0(a, sx) + dev0(b, s)))
                 )
            );
  Real y = (0.5 - x) + 0.5;
  if (xm1) std::swap(x,y);
  // check factor
  if (!bt) return lower_tail ? 0. : 1.;
  // parameters
  int n = 1;
  Real sum = 0.0, c= 1., term;
  do
  {
    sum += (term =  (c *= (1.-b/n)*x) / (a+n));
    ++n;
  }
  while (std::abs(term) > std::abs(sum) * Arithmetic<Real>::epsilon());
  // return result
  return lower_tail ? bt*(1./a + sum) : (1.-bt/a-bt*sum);
}
 
static Real serie_up( Real const& a, Real const& b, Real x, bool xm1, int n)
{
  // trivial case
  if (n==1) return b1(a, b, x, xm1)/a;
 
  // constants
  Real s = a+b, sx=s*x, sy = s- sx;
  Real x0 = (xm1) ?  (0.5 -x) + 0.5 : x;
  int l = std::min(std::max(0, (int)round( xm1 ? (sy-a+1)/x : (sx-a+1)/x0)), n-1);
  Real sum1 = 0., sum2 = 1., s0 = s+l, a0 = a+l;
  // first serie
  for (int k=n-l-2; k>=0; --k)  { sum2 = 1. + sum2 *x0*(s0+k)/(a0+k+1);}
  // second serie
  if (l>0)
  {
    sum1 = 1.;
    for (int k=1; k<l; ++k) { sum1 = 1.+ sum1*(a+k)/((s+k-1)*x0);}
    sum1 /= ((s0-1)*x0);
  }
  // return result
  return b1(a+l, b, x, xm1) *(sum2/a0 + sum1);
}
 
Real betaRatio_up( Real const& a, Real const& b, Real const& x
                        , bool xm1, bool lower_tail
                        )
{
#ifdef STK_BETARATIO_DEBUG
  stk_cout << _T("BetaRatio_up(") << a << _T(", ") << b << _T(", ") << x << _T(")\n");
#endif
  // number of iterations
  int n = int(a);
  // compute residual
  Real a0 = a-n;
  // zero case
  if (!a0) { --n; a0=1.;}
  // sum
  Real c=  serie_up(a0, b, x, xm1, n) * (lower_tail ? - 1. : 1.);
  return (b<=15) ? betaRatio_sr(a0, b, x, xm1, lower_tail) +c
                 : betaRatio_ae(b, a0, x, !xm1, !lower_tail) +c;
}
 
Real betaRatio_cf( Real const& a, Real const& b, Real x
                 , bool xm1, bool lower_tail
                 )
{
#ifdef STK_BETARATIO_DEBUG
  stk_cout << _T("BetaRatio_cf(") << a << _T(", ") << b << _T(", ") << x << _T(")\n");
#endif
  // parameters
  Real s  = a+b, sx = s*x, sy = s-sx;
  /* Compute the function:
   *  B(a,b,x,y) = \frac{ x^{a} (1-x)^{b}}{B(a,b)}
   *  using  (a+b) * (p*log(x/p)+q*log(y/q))
   */
  Real bt = b1(a, b, x, xm1);
  if (bt*Arithmetic<Real>::epsilon() == 0.) return lower_tail ? 0. : 1.;
 
  // initialize numerator
  Real Nold = 0, Ncur = 1.; // = a_1 = 1
  // initialize denominator
  Real Dold = 1., Dcur = xm1 ? 1.-sy/(a+1.) : 1.-sx/(a+1.); // = b_1
  // normalize if necessary
  if (std::abs(Dcur) > 4294967296.)
  {
    Ncur /= Dcur;
    Dold /= Dcur;
    Dcur = 1.;
  }
  // auxiliary constant variables
  const Real    x_4 = xm1 ? (0.125 - x/4.) + 0.125 : x/4.;
  const Real cte_b1 = xm1 ? x/2. + 0.5 : (0.5 - x/2.) + 0.5;
  const Real cte_b2 = xm1 ? (a-1.)*(b+s-1.)*((0.25-x/2.)+0.25) : (a-1.)*(b+s-1.)*x/2.;
  const Real cte_a1 = a*(a-2.)*(b+s)*(b+s-2.), cte_a2 = (a-1.)*(b+s-1.)*x_4;
  // result
  Real cf = 1/Dcur;
  // auxiliary variables
  Real ap2n = a+2., ap2nm1 = a+1.,ap2nm2 = a;
  // iterations
  for (int n=1; /*n<=iterMax*/; n++, ap2n += 2., ap2nm1 += 2., ap2nm2 += 2.)
  {
    // compute a_n
    Real a_n = (cte_a2/ap2nm1 - x_4) * (x_4 + cte_a2/ap2nm1) - cte_a1*(x_4/ap2n)*(x_4/ap2nm2) ;
    // check trivial case
    if (a_n*Arithmetic<Real>::epsilon() == 0.) break;
    // compute b_n
    Real b_n = cte_b1 - cte_b2/(ap2nm1*(ap2n+1));
    // compute numerator and denominator
    Real anew = b_n * Ncur + a_n * Nold;
    Nold = Ncur;
    Ncur = anew;
    // check for underflow
    if (Ncur*Arithmetic<Real>::epsilon() == 0.) { cf =0.; break;}
    anew = b_n * Dcur + a_n * Dold;
    Dold = Dcur;
    Dcur = anew;
    // normalize if necessary
    if (std::abs(Dcur) > 4294967296.)
    {
      Ncur /= Dcur;
      Nold /= Dcur;
      Dold /= Dcur;
      Dcur = 1.;
    }
    // normalize if necessary with 2^32
    if (std::abs(Ncur) > 4294967296.)
    {
      Ncur /= 4294967296.;
      Nold /= 4294967296.;
      Dold /= 4294967296.;
      Dcur /= 4294967296.;
    }
    // test D_n not too small
    if (std::abs(Dcur) != 0)
    {
      Real cfold = cf;
      cf = Ncur/Dcur;
      // check cv
      if (std::abs(cf - cfold) < std::abs(cf)*Arithmetic<Real>::epsilon()) { break;}
    }
  }
  return lower_tail ? bt*cf/a : 1-bt*cf/a;
}
 
static Real coefs_odd_se(std::vector<Real> &A)
{
  // get the index of the current coefficient (should be n = 2 * l with l>=1)
  int n = A.size()-1;
  int l = n/2;
 
  // initialize the sums
  Real U2lp1 =A[1]*A[n-1], T2lp1 =0;
  for (int k=2; k<l; k++)
  {
    U2lp1 += A[k] * A[n-k];
    T2lp1 += A[k+1]*A[n+1-k];
  }
  // compute the result
  Real res = -( A[2]*A[n]*(n-1.)
              + 2* U2lp1 + (n+2.) * T2lp1
              + A[l]*A[l] + (l+1.) * A[l+1]*A[l+1]
              ) / ((n+2.) * A[1]);
  // save it in A
  A.push_back(res);
  // and return it
  return res;
}
 
static Real coefs_even_se( std::vector<Real> &A)
{
  // get the current coefficient (should be n = 2 * l - 1 with l>=1)
  int n = A.size()-1;
  int l = (n+1)/2;
  // initialize the sums
  Real U2l =A[1]*A[n-1], T2l =0;
  // update sum
  for (int k=2; k<l; k++)
  {
    U2l += A[k]*A[n-k];
    T2l += A[k+1] *A[n+1-k];
  }
  // compute the result
  Real res = -(A[2]*A[n]*(n-1.) + 2.*U2l + (n+2.) * T2l ) / ((n+2.) * A[1]);
  // save it in A
  A.push_back(res);
  // and return it
  return res;
}
 
/* @ingroup Analysis
 *  @brief compute the coefficients of the beta Ratio function
 *  asymptotic expansion.
 *
 *  Given the n=2l+1 first coefficients, compute and return the (2l+2)-th
 *  coefficient. The value is stored to the back of the Vector.
 *
 *  @param A vector of dimension 0:n, n=5,7,... of the coefficients
 *  @return the (n+1)-th coefficient
 */
//static Real coefs_se( std::vector<Real> &A)
//{
//  // get the number of existing coefficient
//  int n = A.size();
//  // sum
//  Real Sn =2*A[1]*A[n-2];
//  for (int k=2; k<=n-3; k++)
//  { Sn += (k+1) * A[k+1]*A[n-k] + A[k] * A[n-1-k];}
//  // compute the result
//  Real res = -((n-2.)*A[2]*A[n-1]/A[1] + Sn/A[1]) / (n+1.);
//  // save it in A
//  A.push_back(res);
//  // and return it
//  return res;
//}
 
Real betaRatio_se( Real const& a, Real const& b, Real const& x
                 , bool xm1, bool lower_tail
                 )
{
#ifdef STK_BETARATIO_DEBUG
  stk_cout << _T("BetaRatio_se(") << a << _T(", ") << b << _T(", ") << x << _T(")\n");
#endif
  // parameters
  Real s  = a+b, p  = a/s, q  = b/s, sx = s*x, sy = s-sx;
  //Real z2  = 2 * (a+b) (p*log(x/p)+q*log(y/q));
  Real z2 = 2. * (xm1 ? dev0(a, sy)+dev0(b, sx) : dev0(a, sx)+dev0(b, sy));
  Real z  = (((x<p)&&!xm1)||((x>q)&&xm1)) ? -std::sqrt(z2) : std::sqrt(z2);
  //  Compute normal cdf
  Real pnorm = lower_tail ?  normal_cdf_raw( z) : normal_cdf_raw(-z);
  //  Compute normal pdf
  Real dnorm = Const::_1_SQRT2PI_ * exp(-z2/2.);
  // check large values of z
  if (dnorm < Arithmetic<Real>::epsilon()) return pnorm;
 
  // auxiliary variables
  Real a1 = std::sqrt(a)*std::sqrt(b)/s, a2 = (b - a)/(3.*s), a2_a1 = a2/a1, sqrts = std::sqrt(s);
 
  // series coefs
  std::vector<Real> A, B;
  A.reserve(10); // reserve enough space
  A.push_back(p); // a0
  A.push_back(a1); // a1
  A.push_back(a2); // a2
  A.push_back(a1 * (a2_a1/2.+0.5) * (a2_a1/2.-0.5)); //a3
  A.push_back(-0.4*a2*((a2_a1/2.+0.5) * (a2_a1/2.-0.5)+1.)); // a4
  // compute the numerator and the denominator
  Real num = (a2 * 2.
             + (A[3] * 3. * z
               + (A[4] * 4. * (2+ z2)
                 + (coefs_odd_se(A) * 5. * z * (3 + z2)
                   + (coefs_even_se(A) * 6. * (2*4 + z2 * (4. + z2))
                     + (coefs_odd_se(A) * 7. * z *(5*3 + z2*(5 + z2))
                       + (coefs_even_se(A) * 8. * (2*4*6 + z2 * (4*6 + z2 *(6 + z2)))
                         + (coefs_odd_se(A) * 9. * z * (7*5*3 + z2 * (7*5 + z2 * (7+z2)))
                             + (coefs_even_se(A) * 10. * (2*4*6*8 + z2 * (4*6*8 + z2 *(6*8 + z2 * (8 + z2))))
                               + (coefs_odd_se(A) * 11. * z * (9*7*5*3 + z2 * (9*7*5 + z2 * (9*7+z2 * (9 + z2))))
                               )/sqrts)/sqrts)/sqrts)/sqrts)/sqrts)/sqrts)/sqrts)/sqrts)/sqrts)/sqrts;
  Real den = a1 + (A[3] + (A[5] + (A[7] + (A[9] + A[11] * 11./s) * 9./s)*7./s)*5./s)*3./s;
 
  // compute ratio
  Real ratio = num/den;
  // result
  return lower_tail ? pnorm - ratio * dnorm : pnorm + ratio * dnorm;
}
 
/* @ingroup Analysis
 *  Compute the beta ratio function.
 *  \f[
 *     I_x(a,b) = \frac{\int_0^x u^{a-1} (1-u)^{b-1}}{\int_0^\infty u^{a-1} (1-u)^{b-1}} du
 *  \f]
 *  for \f$ 0\leq x \leq 1\f$.
 *
 *  @param a, b first and second parameters, must be >0
 *  @param x value to evaluate the function
 *  @param lower_tail @c true if we want the lower tail, @c false otherwise
 **/
Real betaRatio( Real const& a, Real const& b, Real const& x, bool lower_tail)
{
  // Check if a and x are available
  if (  isNA(a) || isNA(b) || isNA(x) ) return Arithmetic<Real>::NA();
  // Negative parameter not allowed
  if ((a<=0)||(b<=0))
    STKDOMAIN_ERROR_2ARG(Funct::betaRatio,a,b,negative or null parameters not allowed);
  return betaRatio_raw(a,b,x,lower_tail);
}
Real betaRatio_raw( Real const& a, Real const& b, Real const& x, bool lower_tail)
{
  // trivial case
  if (x<=0) return lower_tail ? 0. : 1.;
  if (x>=1) return lower_tail ? 1. : 0.;
  // parameters
  Real p=a/(a+b);
  // small a,b max(a,b) <= 15
  if (std::max(a,b)<=15)
  {
    if ((a<=1 && x <=0.5)||(b<=1 && x>=0.5))
    {
      return (x <=0.5) ? betaRatio_sr(a, b, x, false, lower_tail)
                       : betaRatio_sr(b, a, x, true, !lower_tail);
    }
   // (a<=1) and (x>0.5), use serie_up for b
   if (a<=1) return betaRatio_up(b, a, x, true, !lower_tail);
   // (b<=1) and (x<0.5), use serie_up for a
   if (b<=1) return betaRatio_up(a, b, x, false, lower_tail);
   // min(a,b)>1, use serie_up for a or b
   return (x <=0.5) ? betaRatio_up(a, b, x, false, lower_tail)
                    : betaRatio_up(b, a, x, true, !lower_tail);
  }
  // min(a,b) < 1 and max(a,b) > 15
  if (std::min(a,b)<=1)
  {
//    std::cout << "case 1" << std::endl;
    // case b<=1 and a>=15
    if (a>=15) return betaRatio_ae(a, b, x, false, lower_tail);
    // case a<=1 and b>=15
    if (b>=15) return betaRatio_ae(b, a, x, true, !lower_tail);
  }
 
  // ((1<a<=60)) or ((1<b<=60))
  if ((std::min(a,b)<=60))
  {
//      std::cout << "case 3.2" << std::endl;
    return (a<b) ? betaRatio_up(a, b, x, false, lower_tail)
                 : betaRatio_up(b, a, x, true, !lower_tail);
  }
  // general case
  if ((x<0.97*p)||(x>1.03*p))
  {
//      std::cout << "case 2.1" << std::endl;
    return (x < p) ? betaRatio_cf(a, b, x, false, lower_tail)
                   : betaRatio_cf(b, a, x, true, !lower_tail);
  }
//      std::cout << "case 2.2" << std::endl;
  return (a<b) ? betaRatio_se(a-1, b-1, x, false, lower_tail)
               : betaRatio_se(b-1, a-1, x, true, !lower_tail);
}
 
} // namespace Funct
 
} // namespace STK
 
#undef d1
#undef d2
#undef d3
#undef d4
#undef d5
#undef d6
#undef d7
#undef d8
 
#endif /* not IS_RTKPP_LIBRARY */

d6

#define d6

(

z

)

Value:

              (z*(z*(z*(z*(z/46080.-1./7680.)+143./403200.) \
              -59./112000.)+7999./19404000.)-691./5255250.)

Definition at line 48 of file STK_Funct_betaRatio.cpp.

d7

#define d7

(

z

)

Value:

              (z*(z*(z*(z*(z*(z/645120.-1./76800.)+41./806400.) \
              -11./96000.)+5941./38808000.)-2357./21021000.)+6./175175.)

Definition at line 50 of file STK_Funct_betaRatio.cpp.

d8

#define d8

(

z

)

Value:

              (z*(z*(z*(z*(z*(z*(z/10321920.-1./921600.)+37./6451200.) \
              -73./4032000.)+224137./6209280000.)-449747./10090080000.) \
              +52037./1681680000.)-10851./1191190000.)

Definition at line 52 of file STK_Funct_betaRatio.cpp.