Arithmetic properties of STK fundamental types. More...

#include <STK_Arithmetic.h>

Inheritance diagram for STK::Arithmetic< Type >:

Static Public Member Functions
static Type	NA () throw ()
	Adding a Non Available (NA) special number.

static bool	isNA (Type const &x) throw ()

static bool	isInfinite (Type const &x) throw ()

static bool	isFinite (Type const &x) throw ()

Static Public Attributes
static const bool	hasNA = false
	True if the type has a representation for a "Not Available."

Detailed Description

template<class Type>
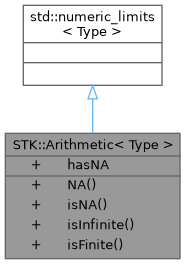
struct STK::Arithmetic< Type >

Arithmetic properties of STK fundamental types.

This class allows a program to obtain information about the representation of a STK fundamental type on a given platform. For non-fundamental STK types, the functions will return 0 and the data members will all be false.

A NA (Not Available) type is defined. If the fundamental type have a quiet_NaN, a NA is a quiet_NaN and the quiet_NaN is no more available.
If the fundamental type does not have a NaN, the greatest value is used.
If the fundamental type is an Integral type (union), a NA is the value (if any) defined in the declaration.

The class arithmetic<Type> inherit from std::numeric_limits<Type> whom which we give hereafter the definition.

  template<typename _Tp>
  struct numeric_limits
  {
    // This will be true for all fundamental types (which have
    // specializations), and false for everything else.
    static const bool is_specialized = false;
 
    // The number of @c radix digits that be represented without change:  for
    // integer types, the number of non-sign bits in the mantissa; for
    // floating types, the number of @c radix digits in the mantissa.
    static const int digits = 0;
 
    // The number of base 10 digits that can be represented without change.
    static const int digits10 = 0;
 
    // True if the type is signed.
    static const bool is_signed = false;
 
    // True if the type is integer.
    static const bool is_integer = false;
 
    // True if the type uses an exact representation.  "All integer types are
    //  exact, but not all exact types are integer.  For example, rational and
    //  fixed-exponent representations are exact but not integer."
    //  [18.2.1.2]/15
    static const bool is_exact = false;
 
    // For integer types, specifies the base of the representation.  For
    // floating types, specifies the base of the exponent representation.
    static const int radix = 0;
 
    // The minimum negative integer such that @c radix raised to the power of
    // (one less than that integer) is a normalized floating point number.
    static const int min_exponent = 0;
 
    // The minimum negative integer such that 10 raised to that power is in
    // the range of normalized floating point numbers.
    static const int min_exponent10 = 0;
 
    // The maximum positive integer such that @c radix raised to the power of
    // (one less than that integer) is a representable finite floating point
    // number.
    static const int max_exponent = 0;
 
    // The maximum positive integer such that 10 raised to that power is in
    //    the range of representable finite floating point numbers.
    static const int max_exponent10 = 0;
 
    // True if the type has a representation for positive infinity.
    static const bool has_infinity = false;
 
    // True if the type has a representation for a quiet (non-signaling)
    // "Not a Number."
    static const bool has_quiet_NaN = false;
 
    // True if the type has a representation for a signaling
    //    "Not a Number."
    static const bool has_signaling_NaN = false;
 
    // See std::float_denorm_style for more information.
    static const float_denorm_style has_denorm = denorm_absent;
 
    // "True if loss of accuracy is detected as a denormalization loss,
    //    rather than as an inexact result." [18.2.1.2]/42
    static const bool has_denorm_loss = false;
 
    // True if-and-only-if the type adheres to the IEC 559 standard, also
    // known as IEEE 754.  (Only makes sense for floating point types.)
    static const bool is_iec559 = false;
 
    // "True if the set of values representable by the type is finite. All
    // built-in types are bounded, this member would be false for arbitrary
    // precision types." [18.2.1.2]/54
    static const bool is_bounded = false;
 
    // True if the type is @e modulo, that is, if it is possible to add two
    // positive numbers and have a result that wraps around to a third number
    // that is less.  Typically false for floating types, true for unsigned
    // integers, and true for signed integers.
    static const bool is_modulo = false;
 
    // True if trapping is implemented for this type.
    static const bool traps = false;
 
    static const bool tinyness_before = false;
 
    // See std::float_round_style for more information.  This is only
    // meaningful for floating types; integer types will all be
    // round_toward_zero.
    static const float_round_style round_style = round_toward_zero;
 
    // The minimum finite value, or for floating types with
    // denormalization, the minimum positive normalized value.
    static _Tp min() throw() { return static_cast<_Tp>(0); }
 
    // The maximum finite value.
    static _Tp max() throw() { return static_cast<_Tp>(0); }
 
    // The @e machine @e epsilon:  the difference between 1 and the least
    //value greater than 1 that is representable.
    static _Tp epsilon() throw() { return static_cast<_Tp>(0); }
 
    // The maximum rounding error measurement (see LIA-1).
    static _Tp round_error() throw() { return static_cast<_Tp>(0); }
 
    // The representation of positive infinity, if @c has_infinity.
    static _Tp infinity() throw()  { return static_cast<_Tp>(0); }
 
    // The representation of a quiet "Not a Number," if @c has_quiet_NaN.
    static _Tp quiet_NaN() throw() { return static_cast<_Tp>(0); }
 
    // The representation of a signaling "Not a Number," if
    // @c has_signaling_NaN.
    static _Tp signaling_NaN() throw() { return static_cast<_Tp>(0); }
 
    // The minimum positive denormalized value.  For types where
    // @c has_denorm is false, this is the minimum positive normalized
    //  value.
    static _Tp denorm_min() throw() { return static_cast<_Tp>(0); }
};